GENERATION OF PHYSICS |
| SOAL DAN PEMBAHASAN KINEMATIKA DENGAN ANALISIS VEKTOR Posted: 18 Sep 2013 07:32 PM PDT KINEMATIKA GERAK LURUS Soal No. 1 Sebuah partikel bergerak dengan persamaan posisi terhadap waktu : r(t) = 3t2 − 2t + 1 dengan t dalam sekon dan rdalam meter. Tentukan: a. Kecepatan partikel saat t = 2 sekon b. Kecepatan rata-rata partikel antara t = 0 sekon hingga t= 2 sekon Pembahasan a. Kecepatan partikel saat t = 2 sekon (kecepatan sesaat)  b. Kecepatan rata-rata partikel saat t = 0 sekon hingga t = 2 sekon  | ||||||||||
| SOAL DAN PEMBAHASAN PIPA ORGANA Posted: 18 Sep 2013 07:33 PM PDT  KONSEP DASAR: KONSEP DASAR:
Soal No. 1 Sebuah pipa organa yang terbuka kedua ujungnya memiliki nada dasar dengan frekuensi sebesar 300 Hz. Tentukan besar frekuensi dari : a) Nada atas pertama b) Nada atas kedua c) Nada atas ketiga Pembahasan Perbandingan nada-nada pada pipa organa terbuka (POB) memenuhi:
fo adalah frekuensi nada dasar f1 adalah frekuensi nada atas pertama f2 adalah frtekuensi nada atas kedua dan seterusnya. Perhatian ! (Sesuaikan lambang-lambang jika terdapat perbedaan, sebagian literature melambangkan nada dasar sebagai f1) a) Nada atas pertama (f1) f1 / fo = 2/1 f1 = 2 × fo = 2× 300 Hz = 600 Hz b) Nada atas kedua ( f2) f2/ fo = 3 / 1 f2 = 3 × fo = 3 × 300 = 900 Hz c) Nada atas ketiga f3/ fo = 4 / 1 f3 = 4 × fo = 4 × 300 = 1200 Hz Soal No. 2 Sebuah pipa organa yang tertutup salah satu ujungnya memiliki nada dasar dengan frekuensi sebesar 300 Hz. Tentukan besar frekuensi dari : a) Nada atas pertama b) Nada atas kedua c) Nada atas ketiga Pembahasan Perbandingan nada-nada pada pipa organa tertutup (POT) memenuhi:
fo adalah frekuensi nada dasar f1 adalah frekuensi nada atas pertama f2 adalah frtekuensi nada atas kedua a) Nada atas pertama (f1) f1 / fo = 3/1 f1 = 3 × fo = 3 × 300 Hz = 900 Hz b) Nada atas kedua ( f2) f2/ fo = 5 / 1 f2 = 5 × fo = 5 × 300 = 1500 Hz c) Nada atas ketiga f3/ fo = 7 / 1 f3 = 7 × fo = 7 × 300 = 2100 Hz Soal No. 3 Seutas dawai memiliki nada atas ketiga dengan frekuensi sebesar 600 Hz. Tentukan : a) frekuensi nada atas kedua dawai b) frekuensi nada dasar dawai Pembahasan Perbandingan nada-nada pada dawai, sama dengan perbandingan nada-nada pada pipa organa terbuka yaitu memenuhi:
Sehingga: a) frekuensi nada atas kedua dawai f2 f2 / f3 = 3 / 4 f2 = ( 3 / 4 )× f3 = (3/4) x 600 = 450 Hz b) frekuensi nada dasar dawai fo fo / f3 = 1 / 4 fo = ( 1 / 4 ) × f3 = (1/4) x 600 = 150 Hz Soal No. 4 Sebuah pipa organa tertutup memiliki panjang 50 cm. Jika cepat rambat bunyi di udara adalah 340 m/s, tentukan frekuensi pipa organa saat: a) terjadi nada dasar b) terjadi nada atas kedua Pembahasan Data: Pipa Organa Tertutup L = 50 cm = 0,5 m ν = 340 m/s a) fo = .....Hz b) f2 = .....Hz Agar tidak terlalu banyak rumus yang harus dihafal, perhatikan ilustrasi berikut:
Untuk selanjutnya rumus yang akan digunakan adalah rumus yang sudah kita kenal sebelumnya, yaitu:
a) Dari ilustrasi diatas terlihat, saat terjadi nada dasar, pada pipa sepanjang L terjadi 1/4 gelombang. L = 1/4 λ atau λ = 4L = 4(0,5) = 2 m Sehingga: f = ν / λ = 340 / 2 = 170 Hz Frekuensi yang kita temukan ini adalah frekuensi nada dasar atau fo a) Dari ilustrasi diatas terlihat, saat terjadi nada atas kedua, pada pipa sepanjang L terjadi 5/4 gelombang. L = 5/4 λ atau λ = 4/5 L = 4/5 (0,5) = 0,4 m Sehingga: f = ν / λ = 340 / 0,4 = 850 Hz Frekuensi yang kita temukan ini adalah frekuensi nada atas kedua atau f2 Soal No. 5 Sebuah pipa organa terbuka memiliki panjang 60 cm. Jika cepat rambat bunyi di udara adalah 340 m/s, tentukan frekuensi pipa organa saat terjadi nada atas kedua Pembahasan Sketsa nada-nada pada pipa organa terbuka:
Saat terjadi nada atas kedua, terlihat pada pipa organa sepanjang L terbentuk satu setengah atau 3/2 gelombang, L = 3/2 λ atau λ = 2/3 L = 2/3 × 0,6 = 0,4 m Sehingga: f = ν / λ = 340 / 0,4 = 850 Hz Frekuensi yang kita temukan ini adalah frekuensi nada atas kedua atau f2 Soal No. 6 Diberikan dua buah pipa organa yang pertama tertutup salah satu ujungnya, satu lagi terbuka kedua ujung dengan panjang 30 cm. Jika nada atas kedua pipa organa tertutup sama dengan nada atas ketiga pipa terbuka, tentukan panjang pipa organa yang tertutup! Pembahasan Pipa organa tertutup: Nada atas kedua → L = 5/4 λ → λ = 4/5 L f = ν / λ f = ν / (4/5 L) Pipa organa terbuka: Nada atas ketiga → L = 2 λ → λ = 1/2 L = 1/2 (30) = 15 cm f = ν / λ f = ν / 15 Frekuensi kedua pipa adalah sama, disamakan saja:  Soal No. 7 Pipa organa terbuka A dan pipa organa tertutup-sebelah B mempunyai panjang yang sama. Perbandingan frekuensi nada atas pertama antara pipa organa A dan pipa organa B adalah.... A. 1 : 1 B. 2 : 1 C. 2 : 3 D. 3 : 2 E. 4 : 3 (UMPTN 1995) Pembahasan Pipa organa A terbuka: Nada atas 1 → L = λ → λ = L f = ν / L Pipa organa B tertutup: Nada atas 1 → L = 3/4 λ → λ = 4/3 L f = ν / (4/3 L) maka  Sumber: fisikastudycenter.com |
| You are subscribed to email updates from GENERASI FISIKA SMA MA To stop receiving these emails, you may unsubscribe now. | Email delivery powered by Google |
| Google Inc., 20 West Kinzie, Chicago IL USA 60610 | |








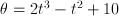 Tentukan:
Tentukan:
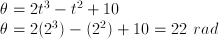
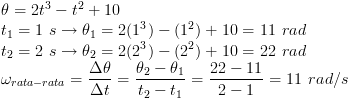
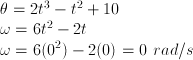

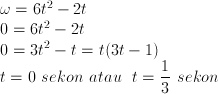

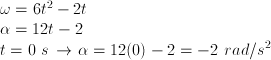




0 Komentar:
Posting Komentar
1. Silahkan tulis komentar anda
2. Dikolom 'Beri Komentar Sebagai' pilih saja Name/URL
3. Isilah nama&URL anda. atau *URL bisa dikosongi
4. Poskan komentar
5. Klik tombol LIKE/SUKA pada laman disebelah kanan.
6. Kunjungi tulisan lainnya di bawah ini.